tan求导
- >
- 话题 >
在微积分中,求导是一个重要的概念,它能够帮助我们研究函数的变化规律。本文将重点介绍tan函数的求导方法,帮助读者更好地理解这一概念。

1. 什么是tan函数
tan函数是三角函数中的一种,它代表了角度的正切值。在数学上,tan表示一个角的正切值,它定义为角的对边和邻边的比值。tan函数的定义域为所有实数,但只在某些特定角度上取值,这也是我们需要求导的原因。
2. tan函数的求导公式
对于一般函数来说,求导是计算函数的变化速率的过程。而tan函数的求导可以通过以下公式得到:
d/dx(tan(x)) = sec^2(x)
3. 推导过程
为了理解tan函数求导的原理,我们先来推导一下。我们将tan函数的定义变形如下:
tan(x) = sin(x) / cos(x)
然后,我们对等式两边同时求导,得到:
d/dx(tan(x)) = d/dx(sin(x) / cos(x))
接下来,我们使用商法求导的规则,得到:

d/dx(tan(x)) = (cos(x) * cos(x) - sin(x) * (-sin(x))) / cos^2(x)
化简上述表达式,得到:
d/dx(tan(x)) = (cos^2(x) + sin^2(x)) / cos^2(x)
根据三角恒等式sin^2(x) + cos^2(x) = 1,我们可以将上述表达式进一步简化为:
d/dx(tan(x)) = 1 / cos^2(x)
而1 / cos^2(x)就是sec^2(x)的定义,所以我们最终得到了tan函数的求导公式。
4. 注意事项
在使用tan函数求导的过程中,有几个需要注意的事项。因为tan函数的定义域为所有实数,所以它的导函数也在所有实数上成立。tan函数的导函数与cos函数的平方值有关,这意味着当cos函数的值很小或等于零时,tan函数的导数会趋于无穷大。因此,在求导时需要注意避免出现这种情况。
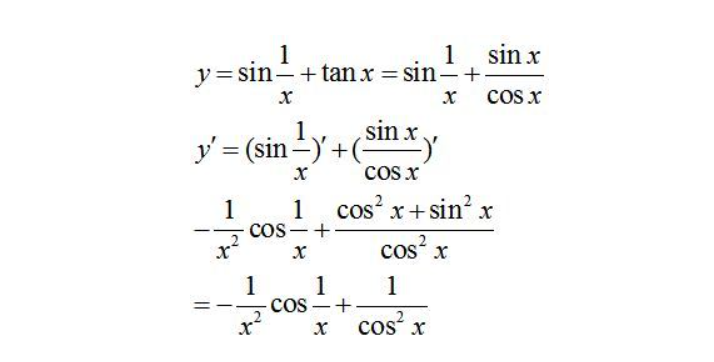
5. 实例解析
为了更好地理解tan函数的求导,我们来看一个实例:求函数f(x) = tan(x)在x = π/4处的导数。
根据tan函数的求导公式,我们有:
f'(x) = d/dx(tan(x)) = sec^2(x)
将x = π/4代入公式中,得到:
f'(π/4) = sec^2(π/4) = 1 / cos^2(π/4)
由于cos(π/4) = sin(π/4) = 1/√2,所以:
f'(π/4) = 1 / (1/√2)^2 = 1 / (1/2) = 2
因此,函数f(x) = tan(x)在x = π/4处的导数为2。
结语:本文通过介绍tan函数的求导方法,帮助读者理解了求导的概念,并举例说明了如何应用求导公式解决实际问题。求导在微积分中起着重要的作用,可以帮助我们研究函数的变化规律,深入理解数学中的各种现象。希望通过本文的介绍,读者能够对tan函数的求导有更深入的了解。
- 发表于 2024-08-19 08:54
- 阅读 ( 395 )
- 分类:默认