矩阵乘法是指对两个矩阵进行乘法运算，它的结果是一个新的矩阵。由于矩阵乘法的特殊性质，它不仅能够描述线性变换和投影等运算，还可以用于求解线性方程组和解析几何等问题。了解和掌握矩阵乘法的计算方法有助于我们更深入地理解线性代数和应用数学。

1. 矩阵的乘法定义和规则

2. 矩阵乘法的计算方法

3. 矩阵乘法的应用举例

1. 矩阵的乘法定义和规则

矩阵乘法的定义非常简单，对于两个矩阵A和B，我们按照行与列的配对方式进行乘法运算，并将结果相加。具体而言，矩阵A的第i行与矩阵B的第j列进行乘法运算，并将结果相加得到新矩阵C中的元素C(i,j)。这一过程可以用数学公式表示为：C(i,j) = ∑(A(i,k) * B(k,j))，其中∑表示对k的求和。

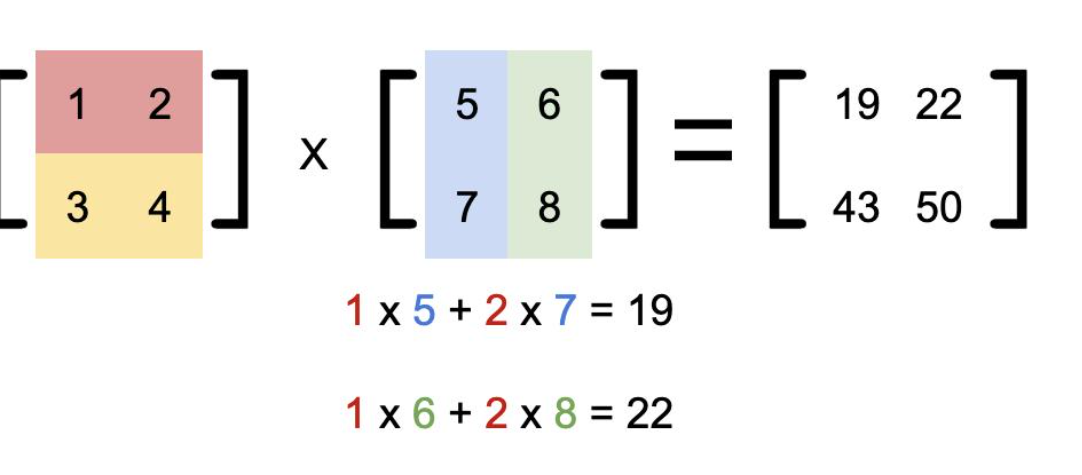
2. 矩阵乘法的计算方法

为了计算矩阵乘法，我们需要明确两个矩阵的维度。假设矩阵A的维度为m×n，矩阵B的维度为n×p，那么矩阵C的维度为m×p。为了得到C的每个元素，我们可以按照以下步骤进行计算：

a. 根据矩阵乘法的定义，遍历A的每一行和B的每一列。

b. 对于A的第i行和B的第j列，按照乘法相加规则，计算A(i,k) * B(k,j)的乘积，并累加到C(i,j)中。

c. 重复以上步骤，直到遍历完所有行和列。

d. 最终得到矩阵C，它是由A和B的乘法运算得到的新矩阵。

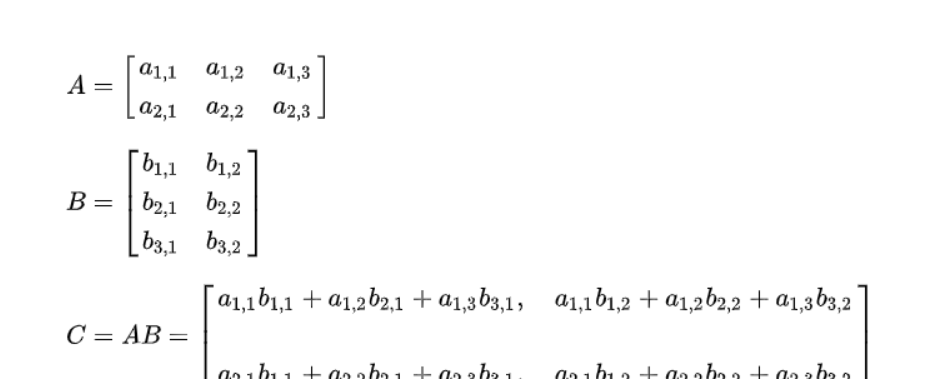
3. 矩阵乘法的应用举例

矩阵乘法的应用非常广泛，下面以两个例子来说明：

a. 线性方程组的求解：对于一组线性方程，可以将其用矩阵形式表示，其中矩阵A包括了方程的系数，向量X表示未知数，向量B表示等式右端常数项。通过矩阵乘法AX=B，我们可以求解出向量X，从而得到方程组的解。

b. 图像处理：在图像处理中，每个像素点可以表示为一个矩阵。通过矩阵乘法，我们可以对图像进行平移、旋转和缩放等线性变换，从而实现图像处理的多种效果。

总结：矩阵乘法是线性代数中的重要概念，它的定义和计算方法很简单，但在实际应用中具有广泛的应用价值。掌握矩阵乘法的计算方法有助于我们更好地理解和运用线性代数的知识，同时也能够帮助我们解决实际问题。无论是在科学研究还是工程实践中，矩阵乘法都是不可或缺的工具。